Meiotic Homolog Pairing¶
In collaboration with the Burgess lab at UC Davis, we are interested in simulating chromosomes diffusing in a budding yeast nucleus in order to compare to their single-particle tracking data of homologous (and heterologous) loci diffusing in early meiosis I.
We don’t have concrete measurements of the viscoelasticity of these nuclei, we will assume they are water-like (i.e. \(\alpha = 1\) in a fractional Langevin model of polymer diffusion). And since we are interested in large-scale motion (frame rate in our real movies is already 30s), we can simply use the Rouse model for the behavior of each chromosome.
Testing Code¶
The :mod:wlcsim.bd.rouse module was originally written by Bruno Beltran to replace Andrew Spakowitz/Steph Weber/Elena Koslover’s FORTRAN77 Brownian dynamics codebase for fractional ssWLC simulation. We want to do some tests so make sure that the new code behaves as expected in all limiting cases with known behavior.
Rouse behavior¶
The simulations should reproduce the Gaussian statistics associated with a Rouse polymer with the given parameters.
This includes an MSD that scales like
and Gaussian inter-bead distributions with mean spacing \(L_0 b\).
In order to see this behavior, we turn off the confinement by setting the strength of the confinement force Aex to 0, and do not tether any beads to the confinement nor pair any loci together
[134]:
import numpy as np
import wlcsim
from wlcsim.bd import rouse, homolog
N = int(1e2+1); L = 17.475; R = 1; b = 0.015; D = 2e1 # ChrV
dt = rouse.recommended_dt(N, L, b, D)
Aex = 0; # no confinement
N_tot, loop_list = homolog.points_to_loops_list(N, []) # no loops
tether_list = np.array([]).astype(int) # no tethered loci
The following derived parameters are explained in the docs for :mod:wlcsim.bd.rouse.
[135]:
Nhat = L/b; L0 = L/(N-1); Dhat = D*N/Nhat; bhat = np.sqrt(L0*b)
Saving all 1e6 time steps doesn’t take up THAT much memory, but calculating the taMSD (a O(N^2) operation) for that many time points is prohibitive.
We use bnp.loglinsample to save sets of equispaced time points (in chunks of length Nlin) that cover all time scales of our simulation. Nlin is chosen to be small enough that O(Nlin^2) is not too big.
You can think of loglinsample as returning a bunch of separate arrays
1) `np.arange(0, dt*Nlin, dt)`
2) `np.arange(0, dt*Nlin**2, Nlin*dt)`
3) ...
4) `np.linspace(0, Nt*dt, Nlin)`
we will compute the MSD using the equally-spaced points in each of these arrays, then recombine that into a single curve below.
[136]:
Nt = 1e6; # total number of equi-space time steps
Nlin = 1e4; # see docstring of loglinsample
t = np.arange(0, Nt*dt, dt) # take Nt time steps
from bruno_util import numpy as bnp
t_i, i_i = bnp.loglinsample(Nt, Nlin, 0.6)
t_save = t[t_i]
[137]:
i_i = [np.round(i).astype(int) for i in i_i] # numba workaround
Simulate for long enough to see the cross-over into the :math:t^{1/2} regime. (This simulation takes about 4min on my laptop).
[139]:
# run actual simulation
x = homolog._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t_save)
Post-processing simulation a score or so seconds per _get_bead_msd call (time averaged MSD calculation is expensive)
[140]:
import wlcsim.bd.runge_kutta
sim_ts = []
sim_msds = []
for i in i_i:
sim_ts.append(t_save[i])
# extract msd of 51st (of 101) bead from simulation
m, c = wlcsim.bd.runge_kutta._get_bead_msd(x[i], 51)
sim_msds.append(m/c)
First plot the MSD curves separately, to demonstrate that the clever time-point choice worked correctly
[141]:
for t, msd in zip(sim_ts, sim_msds):
plt.plot(t[1:], msd[1:])
plt.yscale('log'); plt.xscale('log')
now combine them altogether (this is what you would normally do)
[142]:
sim_msd = np.zeros_like(t_save)
# for each set of equi-spaced time points we used
for i in i_i:
# extract msd of 51st (of 101) bead from simulation
m, c = wlcsim.bd.runge_kutta._get_bead_msd(x[i], 51)
# recombine into single array, overwriting values computed from
# more tightly-space points with those from less tightly-spaced
sim_msd[i[1:]] = m[1:]/c[1:]
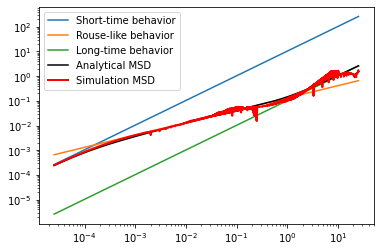
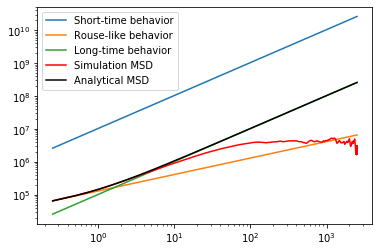
compare MSD curves to analytical result (by truncating/choosing a finite number of modes matching N/2 beads, we recover the exact analytical theory for a finite rouse chain from that of the infinite chain)
[143]:
import matplotlib.pyplot as plt
# exclude t=0 to make log/log msd look good
plt.plot(t_save[1:], 6*D*(N/Nhat)*t_save[1:], label='Short-time behavior')
plt.plot(t_save[1:], 1.9544100*b*np.sqrt(D*t_save[1:]), label='Rouse-like behavior')
plt.plot(t_save[1:], 6*D*t_save[1:]/Nhat, label='Long-time behavior')
plt.plot(t_save[1:], wlcsim.analytical.rouse.rouse_mid_msd(t_save[1:],
b, Nhat, D, num_modes=int(N/2)), 'k', label='Analytical MSD')
plt.plot(t_save[1:], sim_msd[1:], 'r', label='Simulation MSD', lw=2)
plt.yscale('log'); plt.xscale('log');
plt.legend()
[143]:
<matplotlib.legend.Legend at 0x7f3f22d66b50>
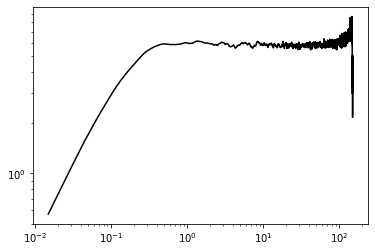
Ornstein-Uhlenbeck test¶
Two-bead chains can be well understood as an Ornstein-Uhlenbeck process in the coordinates of one of the beads. The position autocorrelation of the second bed should be an exponential
[3]:
N = 2; L = 3; R = 1000; b = 1; D = 5 # two O-U processes
dt = rouse.recommended_dt(N, L, b, D)
Aex = 0; # no confinement
N_tot, loop_list = rouse.homolog_points_to_loops_list(N, []) # no loops
tether_list = np.array([]).astype(int) # no tethered loci
we run 100 copies of the process, to get better stats (so 200 total 3D O-U processes, since each simulation has two “homologs”)
[4]:
Nt = 1e4;
t = np.arange(0, Nt*dt, dt) # take Nt time steps
X = []
for i in range(100):
x = rouse._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t)
X.append(np.stack([x[:,1,:] - x[:,0,:], x[:,3,:] - x[:,2,:]]))
X = np.concatenate(X, axis=0)
[7]:
X.shape # (num_samples, num_t, d)
[7]:
(200, 10000, 3)
[6]:
# abuse get_bead_msd, which expects X.shape == (num_t, num_beads, d)
# to get one of the sample's MSDs by pretending its a "bead"
sim_msd, count = wlcsim.bd.runge_kutta._get_bead_msd(np.transpose(X, [1, 0, 2]), 1)
[8]:
plt.plot(t[1:], sim_msd[1:]/count[1:], 'k')
plt.yscale('log'); plt.xscale('log')
[9]:
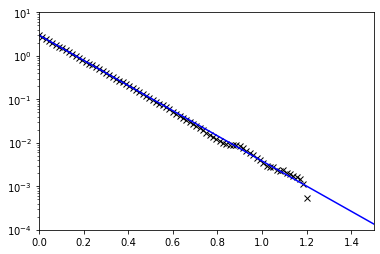
corr, count = wlcsim.bd.runge_kutta._get_vector_corr(X)
[25]:
Nhat = L/b; L0 = L/(N-1); Dhat = D*N/Nhat; bhat = np.sqrt(L0*b)
plt.plot(t, corr/count, 'kx')
kbT_over_k = 3*bhat**2/3 # bhat**2/3 per dimension
k_over_xi = 3*(2*Dhat)/bhat**2 # extra (2*Dhat) because it's two beads tethered, not one tether to origin
plt.plot(t, kbT_over_k * np.exp(-k_over_xi*t), 'b')
plt.yscale('log')
plt.xlim([0, 1.5])
plt.ylim([1e-4, 1e1])
[25]:
(0.0001, 10.0)
Confinement¶
As seen above, if the confinement size is made “weak enough”, the simulation behaves as it should in the absense of a confinement.
The MSD should plateau at the radius of the confinement.
[29]:
N = int(1e2+1); L = 17.475; R = 1.000; b = 0.015; D = 2e1 # ChrV
dt = rouse.recommended_dt(N, L, b, D)
Aex = 100; # multiplier on confinement force
N_tot, loop_list = rouse.homolog_points_to_loops_list(N, []) # no loops
tether_list = np.array([]).astype(int) # no tethered loci
[35]:
Nt = 1e8; Nt_save = 1e4;
t = np.arange(0, Nt*dt, dt) # take Nt time steps
t_save = t[::int(Nt/Nt_save)] # save only a subsample
# run actual simulation
x = rouse._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t_save)
[36]:
# extract msd of 51st (of 101) bead from simulation
sim_msd, count = wlcsim.bd.runge_kutta._get_bead_msd(x, 51)
[37]:
Nhat = L/b; L0 = L/(N-1); Dhat = D*N/Nhat; bhat = np.sqrt(L0*b)
# exclude t=0 to make log/log msd look good
plt.plot(t_save[1:], 6*D*(N/Nhat)*t_save[1:], label='Short-time behavior')
plt.plot(t_save[1:], 1.9544100*b*np.sqrt(D*t_save[1:]), label='Rouse-like behavior')
plt.plot(t_save[1:], 6*D*t_save[1:]/Nhat, label='Long-time behavior')
plt.plot(t_save[1:], sim_msd[1:]/count[1:], 'r', label='Simulation MSD')
plt.plot(t_save[1:], wlcsim.analytical.rouse.rouse_mid_msd(t_save[1:],
b, Nhat, D, num_modes=int(N/2)), 'k', label='Analytical MSD')
plt.yscale('log'); plt.xscale('log');
plt.legend()
[37]:
<matplotlib.legend.Legend at 0x7f0ac12c9710>
Beads that are “tethered” to the confinement should be preferentially “close” to it compared to the rest of the beads in the simulation.
[51]:
N = int(1e2+1); L = 17.475; R = 1.000; b = 0.015; D = 2e1 # ChrV
dt = rouse.recommended_dt(N, L, b, D)
Aex = 100; # multiplier on confinement force
N_tot, loop_list = rouse.homolog_points_to_loops_list(N, []) # no loops
tether_list = np.array([0, 51, 100]).astype(int) # tethered telomeres and centromere
[52]:
%%debug
Nt = 1e6; Nt_save = 1e4;
t = np.arange(0, Nt*dt, dt) # take Nt time steps
t_save = t[::int(Nt/Nt_save)] # save only a subsample
# run actual simulation
x = rouse._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t_save)
NOTE: Enter 'c' at the ipdb> prompt to continue execution.
> <string>(2)<module>()
ipdb> s
> <string>(3)<module>()
ipdb> s
> <string>(4)<module>()
ipdb>
> <string>(6)<module>()
ipdb>
--Call--
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(521)typeof_pyval()
519 return "%s(%s)" % (type(self).__name__, self.py_func)
520
--> 521 def typeof_pyval(self, val):
522 """
523 Resolve the Numba type of Python value *val*.
ipdb> n
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(529)typeof_pyval()
527 # Not going through the resolve_argument_type() indirection
528 # can save a couple µs.
--> 529 try:
530 tp = typeof(val, Purpose.argument)
531 except ValueError:
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(530)typeof_pyval()
528 # can save a couple µs.
529 try:
--> 530 tp = typeof(val, Purpose.argument)
531 except ValueError:
532 tp = types.pyobject
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(534)typeof_pyval()
532 tp = types.pyobject
533 else:
--> 534 if tp is None:
535 tp = types.pyobject
536 return tp
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(536)typeof_pyval()
534 if tp is None:
535 tp = types.pyobject
--> 536 return tp
537
538
ipdb>
--Return--
array(float64, 1d, A)
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(536)typeof_pyval()
534 if tp is None:
535 tp = types.pyobject
--> 536 return tp
537
538
ipdb>
--Call--
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(325)_compile_for_args()
323 return self._compiling_counter
324
--> 325 def _compile_for_args(self, *args, **kws):
326 """
327 For internal use. Compile a specialized version of the function
ipdb> s
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(330)_compile_for_args()
328 for the given *args* and *kws*, and return the resulting callable.
329 """
--> 330 assert not kws
331
332 def error_rewrite(e, issue_type):
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(332)_compile_for_args()
330 assert not kws
331
--> 332 def error_rewrite(e, issue_type):
333 """
334 Rewrite and raise Exception `e` with help supplied based on the
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(345)_compile_for_args()
343 reraise(type(e), e, None)
344
--> 345 argtypes = []
346 for a in args:
347 if isinstance(a, OmittedArg):
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(346)_compile_for_args()
344
345 argtypes = []
--> 346 for a in args:
347 if isinstance(a, OmittedArg):
348 argtypes.append(types.Omitted(a.value))
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(347)_compile_for_args()
345 argtypes = []
346 for a in args:
--> 347 if isinstance(a, OmittedArg):
348 argtypes.append(types.Omitted(a.value))
349 else:
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(350)_compile_for_args()
348 argtypes.append(types.Omitted(a.value))
349 else:
--> 350 argtypes.append(self.typeof_pyval(a))
351 try:
352 return self.compile(tuple(argtypes))
ipdb>
--Call--
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(521)typeof_pyval()
519 return "%s(%s)" % (type(self).__name__, self.py_func)
520
--> 521 def typeof_pyval(self, val):
522 """
523 Resolve the Numba type of Python value *val*.
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(529)typeof_pyval()
527 # Not going through the resolve_argument_type() indirection
528 # can save a couple µs.
--> 529 try:
530 tp = typeof(val, Purpose.argument)
531 except ValueError:
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/dispatcher.py(530)typeof_pyval()
528 # can save a couple µs.
529 try:
--> 530 tp = typeof(val, Purpose.argument)
531 except ValueError:
532 tp = types.pyobject
ipdb>
--Call--
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/typing/typeof.py(24)typeof()
22 _TypeofContext = namedtuple("_TypeofContext", ("purpose",))
23
---> 24 def typeof(val, purpose=Purpose.argument):
25 """
26 Get the Numba type of a Python value for the given purpose.
ipdb>
> /home/bbeltr1/.miniconda/lib/python3.7/site-packages/numba/typing/typeof.py(29)typeof()
27 """
28 # Note the behaviour for Purpose.argument must match _typeof.c.
---> 29 c = _TypeofContext(purpose)
30 ty = typeof_impl(val, c)
31 if ty is None:
ipdb> exit
[42]:
%matplotlib qt5
[43]:
hv = rouse.HomologViewer(x, N, loop_list)
Connectivity¶
If we make the only paired bead be one of the end beads, then the polymers should behave as one long linear polymer.
[ ]:
N = int(1e2+1); L = 17.475; R = 1.000; b = 0.015; D = 2e1 # ChrV
dt = rouse.recommended_dt(N, L, b, D)
Aex = 0; # no confinement
N_tot, loop_list = rouse.homolog_points_to_loops_list(N, [0]) # only one end tethered
tether_list = np.array([]).astype(int) # no tethered loci
[ ]:
x = rouse._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t_save)
The above was verified to work visually using
[ ]:
%matplotlib qt5
hv = rouse.HomologViewer(x, int(N), loop_list)
If we make both end beads be homologously paired, then the two polymers should behave as one larger ring polymer.
[ ]:
N = int(1e2+1); L = 17.475; R = 1.000; b = 0.015; D = 2e1 # ChrV
dt = rouse.recommended_dt(N, L, b, D)
Aex = 0; # no confinement
N_tot, loop_list = rouse.homolog_points_to_loops_list(N, [0, 100]) # only one end tethered
tether_list = np.array([]).astype(int) # no tethered loci
[ ]:
x = rouse._jit_rouse_homologs(N, N_tot, tether_list, loop_list, L, b, D, Aex, R, R, R, t, t_save)
The above was verified to work visually using
[ ]:
%matplotlib qt5
hv = rouse.HomologViewer(x, int(N), loop_list)
Generating Pairing Sites¶
Our simulation as written is purely Brownian Dynamics, (no Gillespie component). This means that we treat the “existing” homolog paired sites as fixed and ask how the polymer fluctuates assuming no new connections are formed.
Thus, our method for choosing which sites are “paired” in a given simulation will greatly affect our results.
By default, all of our simulations will simply choose pairing sites uniformly according to some density FP. That is, each individual bead will have a probability \(0\leq\texttt{FP}\leq1\) of being paired.
However, we present below an alternative strategy for choosing these sites, that involves explicitly simulating the dynamic process of homolog pairing.
\(k_h \lll k_\text{loop}\)¶
In the limit as the rate of polymer loop formation eclipses the rate of stable homolog junction formation (i.e. if it requires many “kissing” events to form a stable homolog junction), then we can treat the homolog pairing process approximately as a Markov chain where the transition rates from a given loci being unpaired to paired simply are proportional to the looping probabilities for the ring polymer defined by its nearest neighbors (where there already exists a junction) to the left and right.
No Unpairing¶
In the case \(k_h \lll k_\text{loop}\) and where we don’t allow unpairing events to occur, we can actually analytically compute the final loop size distribution.
[1]:
#TODO copy from notes to here
[ ]:
Simulations¶
Simulate two rouse chains in confinement, various connectivities.
The ura3 gene is on ChrV, spanning bases 116167–116970. ChrV is 576874 bases, and budding yeast have a mean linker length of 15bp (as estimated based on a nucleosome repeat length (NRL) of ~165bp). This corresponds to a WLC with an effective persistence length of ~15nm in theta-solvent conditions (see Beltran & Kannan et al, PRL 2019). This number has elsewhere been estimated to be as low as 5nm experimentally (Hajjoul et al, Genome Research 2013). Since only 15/165~9% of DNA is in linkers (linear distance along this effective WLC) ChrV’s ~3496 nucleosomes each cover about one third of a Kuhn length. Meaning the chain can be thought of as being made of 1165 Kuhn lengths of 15nm each (for 17475nm total).
So in \(\mu\)m, L=17.475, b=0.015, and N=101 is used to give 100 segments of equal length. (which would make the ura3 locus bead 20).
The nucleus has a radius of about a micron, and loci reach the confinement after about a minute. Because their Rouse diffusion has basically the form \(1.9544100*b*D^{1/2}t^{1/2}\), then we can calculate that \(1^2 \mu{}m^2 = 1.95441 \times 0.015 \mu{}m \times D^{1/2} um/s^{1/2} \times 60^{1/2} s^{1/2}\). In other words, \(D \approx 19.39 \mu{}m^2/s\). So R=1.000, D=2e1.
Notice that since the terminal relaxation time of the polymer is \(N^2 b^2/D\)…
Assuming that we can treat the maximum attained MSD value as the confinement size, approximately, we can just use teh MSD at time 30 as a proxy for the confinement size, since it’s basically flat after that.
If we look at the distribution of these values in the data, we see that the squared displacement has a distribution which is linear
[ ]:
msds = msds.msd(burgess.df_flat, mscd=True, include_z=True, traj_group=burgess.cell_cols, groups=burgess.cell_cols)
m = sds.reset_index()
data = m[m['delta'] == 30]['mean'].values
data = data[~np.isnan(data)]
Y, X = np.histogram(data)
scipy.stats.linregress(X[3:], Y[2:])
the above gives output of
>>> LinregressResult(slope=-648.6107382252995, intercept=1340.988095238095, rvalue=-0.9865990280608326, pvalue=5.956260174887604e-06, stderr=43.79162733110961)
if we don’t square the values, we see that we get a peak at around 0.8um, which I guess will be the mean confinement radius. this is close enough to the current simulation value of ~1um.
If we use t=60, 90, or 120s instead, we still get values around 1um, like 1.02um to 1.12um…